Ohm’s law is one of the fundamentals of electronics and is incredibly handy for quickly calculating the current, voltage, or resistance of a circuit. You will need to know at least two values.

Ohm’s law defines the mathematical relationship between the current, voltage, and resistance of a network.
This law was named after a 19th-century German physicist and mathematician called Georg Ohm. Ohm discovered the relationship back in a time where there was no way of easily measuring current, voltage, or resistance.
Despite being coldly received when first published, it has gone on to become a must-know for anyone interested in electrical circuits. Ohm’s law has become part of the basis for our current understanding of electrical circuitry.
If you’re doing any of our Raspberry Pi electronics projects that involve circuitry then you might find this tutorial handy.
What is Ohm’s Law?
Ohm’s law states that the current passing through a conductor between two points is directly proportional to the voltage across the two points and inversely proportional to the resistance between the two points.
Simply put, if the current is doubled in a circuit, then the voltage is doubled too. Likewise, if the resistance in the circuit is doubled, then the current will fall by half.
While this may sound a little complicated, the actual math behind this theory is incredibly simple to grasp and remember.
Ohm’s Law Formula
Luckily for us, the Ohm’s Law formula is incredibly simple to understand.
Ohm’s law can be expressed as a mathematical formula like below.
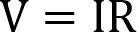
This formula says that voltage (V) is equal to current (I) multiplied by resistance (R).
In all the Ohm’s law formulas, we make use of the following variables.
- V = Voltage, expressed in Volts.
- I = Current, expressed in Amps.
- R = Resistance, express in Ohms.
While the formula can be used to calculate the voltage, it can also be manipulated so that we can instead calculate the current or resistance in the circuit.
To start, let’s first rearrange the formula so that we can calculate the current (I) of a circuit.
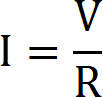
We can also rearrange the base Ohms law formula so that we can calculate the resistance (R) of a circuit.
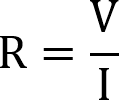
Ohm’s Law Calculator
To make use of this Ohm’s Law calculator, first select whether you want to calculate the voltage, current, or resistance.
With the mode selected, all you need to do is enter the two required values. The calculator will automatically calculate the correct values.
Ohm’s Law Triangle
One of the easiest ways of remembering the three different ohms law formulas is the triangle.

The middle horizontal divider of the triangle represents division, meaning whenever the voltage (V) is involved in the formula, all other letters are divided by it.
For example, if we want to calculate the current (I), we need to divide the voltage (V) by the resistance (R).
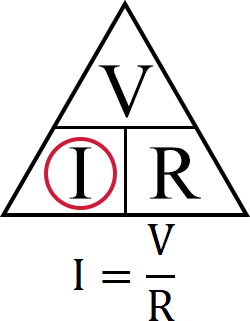
By circling out “I” in the triangle, we can see the formula remains in the triangle with V over R.
We can also use this same triangle to work out the formula for calculating the resistance (R) of a circuit.
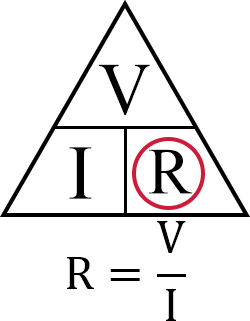
With the resistance (R) circled out we can see the formula we have to use is voltage (V) divided by current (I)
The vertical line in the triangle represents multiplication. This line only ever comes into play when calculating the voltage (V).
Using the Ohm’s law triangle again, we can quickly see the formula we need to use by circling out “V” as that’s the value we want to calculate.
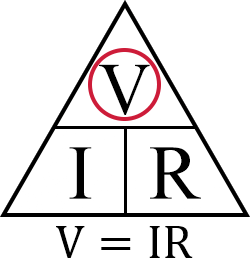
From that, we can easily see that to work out the voltage (V), all we need to do is multiply the current (I) by the resistance (R).
Example of Ohm’s Law in Action
Next, we will be running you through three different circuit examples.
These examples will touch on using each variation of the three different ohms law formulas.
Voltage Example
In this first example, we are going to start with the base ohms law formula to calculate the voltage of a circuit.
To calculate the voltage, we need to know the resistance (R) and the current (I) of the circuit.
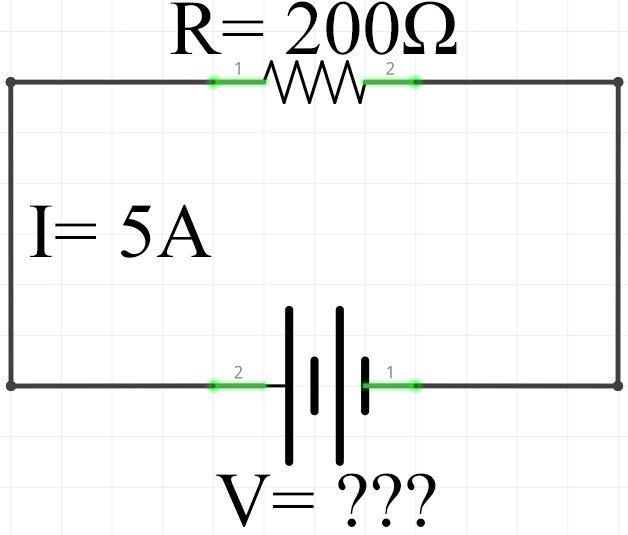
In this example circuit, you can see that we have a resistance (R) of 200 Ohms and a current (I) of 5 Amps.
To calculate the voltage, we need to insert our two values into our ohm’s law formula.
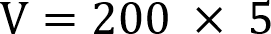
With the formula filled in, you can see that all we need to do is multiply 200 by 5 to calculate the voltage.
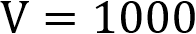
With the resistance and current multiplied together, we can see that the voltage for the example circuit is equal to 1,000 Volts.
Current Example
In this second example, we will be making use of the modified version of the ohms law formula to calculate the current of the following circuit.

From this circuit, we know that the resistance (R) is 50 Ohms and that the voltage (V) is 24 Volts.
We need to put these values into our ohms law formula that has been manipulated to calculate the current (I).
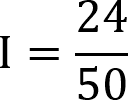
With the resistance and voltage values entered into the formula, we can see that we need to divide 24 by 50 to calculate the current.
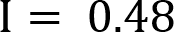
Using Ohm’s law, we calculate the current of the circuit to be 0.48 Amps.
Resistance Example
In our third and final example, we will be making use of the third version of the ohms law formula. In this case, we will be making use of the formula to calculate the resistance of a circuit.
To calculate the resistance of the circuit, we need to know the voltage (V) and the current (I) of the circuit.
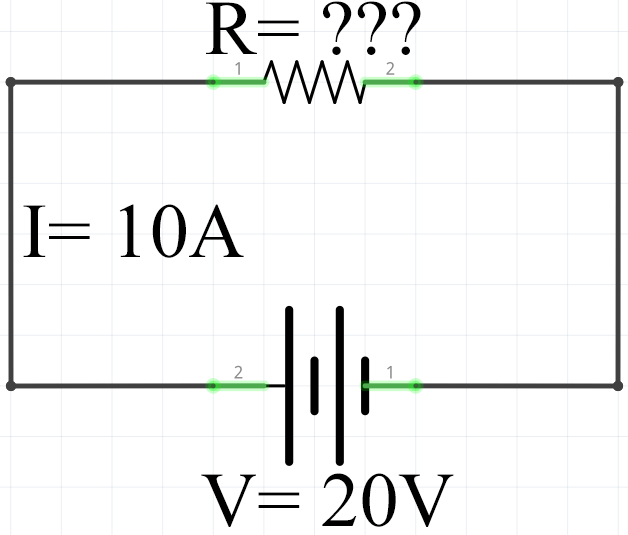
From this example circuit, we can see that our example circuit has a current of 10 Amps and a voltage of 20 Volts.
We need to insert these two values into our Ohm’s Law resistance formula.
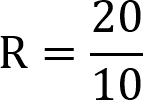
From this, we can calculate the resistance that we need by dividing the voltage of 20 by the 10 amps.
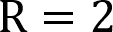
Calculating this out, we can see that the resistance of our example circuit should be 2 Ohms.
Hopefully, at this point, you now have an understanding of Ohm’s Law and how to make use of it. We have worked through how you can utilize Ohm’s law triangle as an easy way of remembering the three different formulas.
You will find these equations very handy in projects that utilize circuitry such as all of our Arduino projects.
If you have any tips or feedback, then feel free to drop a comment below.










Awesome example , super simply stated, thank you.
Thanks for this article. I noticed a typo.
In the current calculation example you give, the text describing the calculation 24/50 reads: “divide 50 by 24 to calculate the current.”
It should read “divide 24 by 50…” (or maybe “ divide 50 into 24”).
50 divided by 24 is 2.0833.
Hi Rob,
Thank you for pointing this out, I have corrected the typo in the guide.
Cheers,
Emmet