In this guide, we will show you how to calculate parallel resistance as well as provide you with an easy to use parallel resistance calculator.

Parallel resistance is a useful part of electronics but can be difficult to calculate when you start dealing with more than two resistors.
Every resistor that you add in parallel reduces the total amount of resistance. This behavior is handy when you need a particular resistance but don’t have a resistor that matches the required value.
The reduction in resistance is caused by the current having more ways of getting through. Each new resistor in parallel allows more current through the circuit and therefore reducing the total resistance that your circuit is facing.
For example, in a circuit with two resistors of equal value in parallel, the resistance will be reduced to exactly half. The math is a bit different for differing resistances and if you have more resistors. We will delve into this later on in the guide.
If you want to increase the resistance of your circuit and not reduce it, then you can use your resistors in series instead.
To help work out the total resistance in a circuit with resistors in parallel, we have a handy calculator that makes the process a lot easier.
If you’re confused by the colors on the resistor, be sure to check out the resistor color code guide as it will teach you everything you need to know.
Parallel Resistance Calculator
To use our parallel resistance calculator, simply set the number of resistors you want to calculate the parallel resistance for. Next, enter the value for each resistor.
The total resistance of your parallel circuit will be calculated and updated as you set the value of each resistor.
Calculating the Total Resistance in Parallel
If you would prefer to learn, you can calculate the resistance of resistors in parallel by hand. The process is a bit tedious and can get complicated fast if you are dealing with several resistors in parallel.
There are three different equations that you can make use of to calculate the total resistance in parallel.
Total Resistance of Two Equal Resistors
The first equation is only to be used when you have two resistors in parallel that have the same resistance.
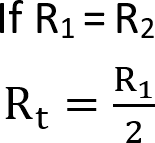
If you have two resistors of the same resistance in parallel, then the total resistance is equal to half of one resistor.
Example Usage of the Equation
For this example, let’s assume that we have two 200 Ohm resistors in parallel, as shown in the circuit below.
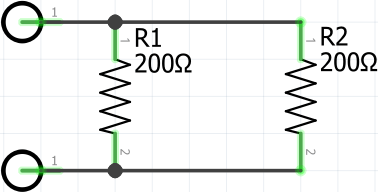
Knowing that there are only two resistors in parallel and that they are of the same value, we can use our equation.
Marking down the R1 value as 200, we can fill in the equation, as we have below. Now, use the equation to calculate the total resistance (Rt).
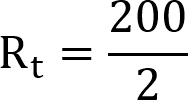
To get the total resistance, all we need to do now is divide our 200 ohm value by 2.
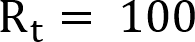
The answer is super easy to work out and is 100.
With that done, you should now have an idea of how to deal with the simplest scenario of two resistors of the same value in parallel.
Total Resistance of Two Differing Resistors
The second equation is a simplified version of the main equation that we use later on. This equation is used when you have two resistors of differing resistance.
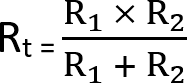
There are a few other processes that you have to go through for calculating the resistance of two resistors in parallel, but it is not drastically more difficult.
Example Usage of the Equation
In this example, we will be assuming we have a circuit with two resistors in parallel of different values.
In this circuit, we have a 600 Ohm resistor and a 250 Ohm resistor in parallel. We now want to work out the total resistance provided by these resistors.
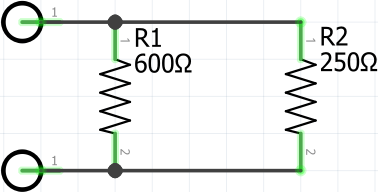
To begin, we need to fill in our equation, with R1 being our 600 ohm resistor and our R2 value being the 250 ohm resistor.
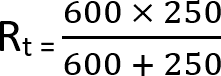
With the equation filled in, we should now do the top multiplication, and the bottom addition before proceeding.
Multiplying 600 (R1) by 250 (R2) should give you a result of 150,000. Adding 600 (R1) to 250 (R2) should give you an answer of 850.
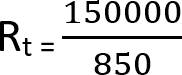
With both values worked out, all we need to do is divide the top number by the bottom number. By doing this, we can work out what the total resistance is of two resistors in parallel.
The math you should be doing with this example is 150,000 divided by 850. From this, you should get a result of 176.47. There will be extra decimal spots, but we will round it to the nearest two.
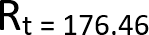
With that done, you should now have an idea of how to calculate the total resistance of two resistors in parallel.
Next, we will show you how to handle three or more resistors. This equation is a slightly more complicated process as it involves a lot of division that results in large decimal numbers.
Total Resistance of Multiple Resistors
The third and final equation that we will be dealing with is the one that you will be using for three or more resistors in parallel.
The equation is rather simple at its core and can be easily extended to deal with a large number of resistors.
The only downside of this equation is that it does get more time consuming the more resistors that you add.
A simple solution is to use a parallel resistor calculator, as we have included above.
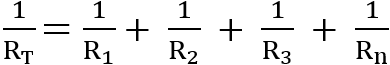
Example Usage of the Equation
In this example, we will show how to make use of the more complicated parallel resistor equation.
For this, we will be using multiple resistors with values of 100 ohms (R1), 250 Ohms (R2), 200 Ohms (R3), and 1K Ohms (R4).
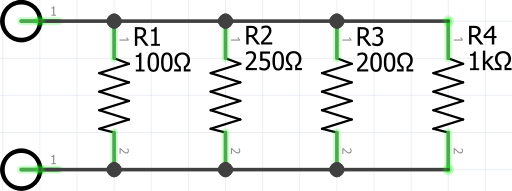
To start, we need to fill in the equation with all our values.
Each of our resistor values will be the divisor for 1, and you can add as many resistors as you need to this equation. For this example, we are only handling four.
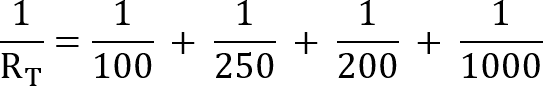
Our next step is to divide 1 by each of our resistor’s values. You must retain as many decimals as possible as precision does affect the final resistance calculation.
For example, in our calculation, we divide 1 by 100, which gives us a result of 0.01.
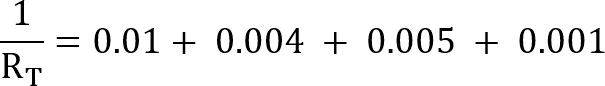
Once you have finished dividing each set of values, we now need to add each value together.
For our example circuit this will mean: 0.01 + 0.004 + 0.005 + 0.001. Luckily for us, this adds up pretty smoothly and gives us a nice round number of 0.02.
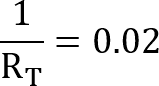
Next, we have to move the divisor from the left hand of the equation over to the right.
This move will mean our calculated value will be become the divisor of 1 and should look like what we have below.
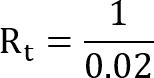
Finally, divide 1 by your divisor, and in our case, is 0.02. This equation will calculate the final total resistance of your resistors in parallel.
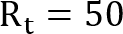
Summary
Hopefully, you now have gathered enough knowledge on how to calculate the total resistance of resistors in parallel. You should find it handy if you plan on doing some Raspberry Pi circuitry projects, or any other kind of electronics project.
If you have any feedback or have any questions regarding this tutorial, then please feel free to post a comment below.
Need faster help? Premium members get priority responses to their comments.
Upgrade for Priority Support









Just above text saying Example use of the equation the left side of the equation should be 1/RT instead of 1/R2. Easily made typo. Good article
Hi Mark,
Thank you for pointing that out!
I have now fixed up that example image so it should be correct now.
Cheers,
Emmet